06. 运动学
运动学
运动学是研究物体运动的学科。运动模型也被称为运动学方程,它提供了预测汽车运动所需的全部信息。
让我们来推导一些最常见的运动模型!
恒定速度
恒定速度模型假定汽车以恒定的速度运动。这是最简单的车辆移动模型。
案例
假设我们的车辆正在以100 m/s 的速度移动,我们想知道它从一个时间 t1 到 t2 移动了多少距离。具体请看下图。
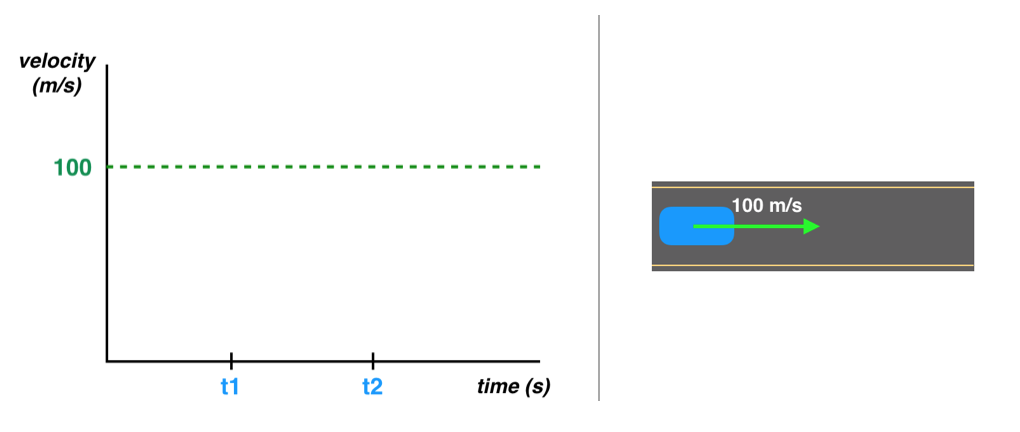
(左)车辆速度图,(右)一辆汽车在路上以 100 m/s 的速度行驶
位移
车辆移动了多少距离叫做 位移 ,我们已经知道如何计算这个了!
例如,我们知道,如果 t2 和 t1 的差是 1 秒,那么车辆移动了
100m/sec*1sec = 100m
。如果 t2 和 t1 的差是 2 秒,那么车辆移动了
100m/sec*2sec = 200m
。
位移始终 =
100m/sec*(t2-t1)
。
移动模型
通常,对于恒定速度,位移的移动模型是:
displacement = velocity*dt
其中,
dt
是“时间差”的微积分符号。
线下面积
回到我们的图,位移也可以看作给定时间区间内的线下面积。
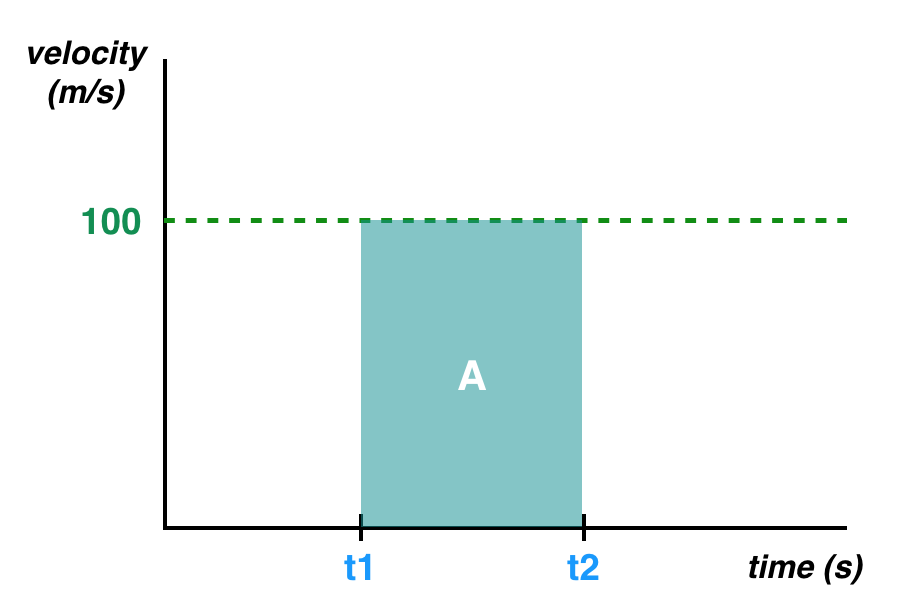
线下面积 A 等于位移!
所以,除了我们的运动模型之外,我们还可以说位移等于线下面积!
displacement = A恒定加速度
恒定加速度模型稍有不同,它假设车辆在不断加速,速度以恒定的速度变化。
假设我们的车辆在 t1 时刻的速度为100 m/s,并且以 10m/s^2 的速率加速。
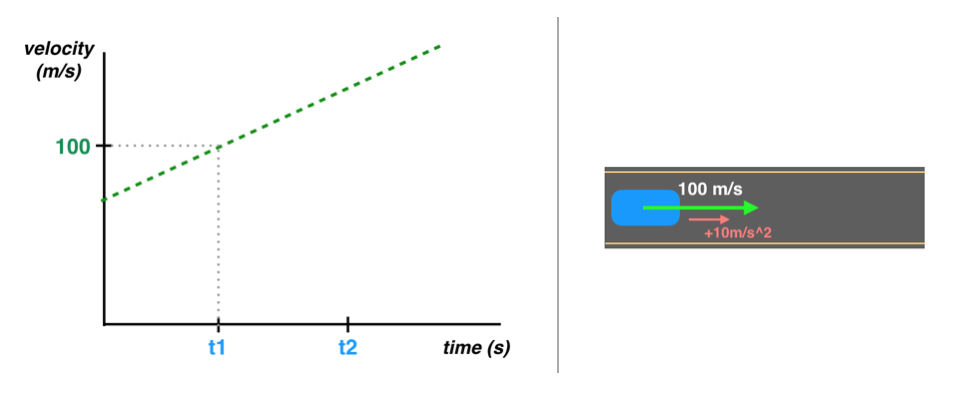
变化速度
对于这个移动模型,我们知道速度在不断变化,每秒增加 10 m/s。这可以用下面的运动学方程表示:
velocity = acceleration*dt位移
位移可以通过计算 t1 和 t2 之间的线下的面积得出,这类似于我们的等速方程,但形状稍微不同。
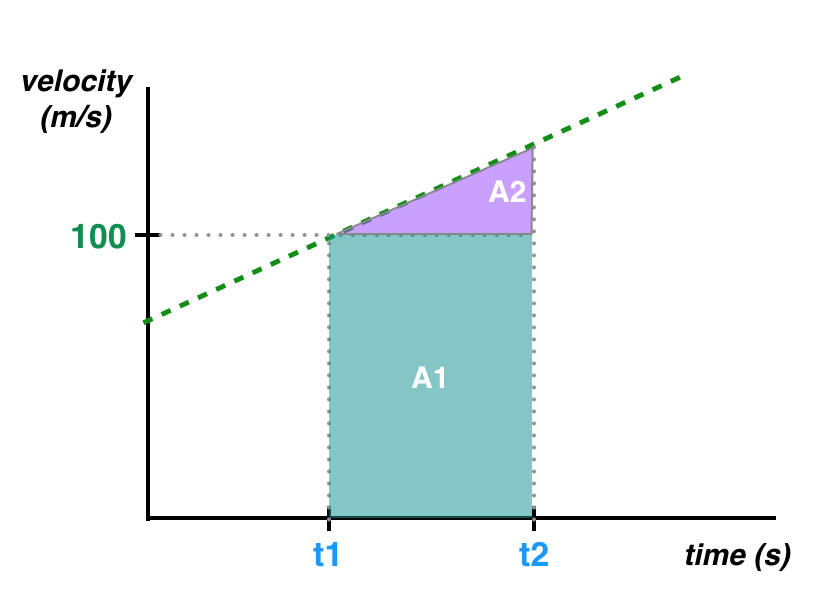
线下面积 A1 和 A2
该面积可以通过将这个区域分成两个不同的形状来计算:一个简单的矩形 A1,以及一个三角形 A2。
A1 与恒定速度模型中的面积相同。
A1 = initial_velocity*dt
换句话说,
A1 = 100m/s*(t2-t1)
。
A2 计算起来有点麻烦。但请记住,三角形的面积是
0.5 * 宽 * 高
。
我们知道,宽度是时间变化 (t2-t1) 或
dt
。
而高度就是这段时间内的速度变化!根据之前的速度方程,我们知道这等于:
加速度 * (t2-t1)
或
加速度 * dt
。
现在我们有了三角形的宽和高,就可以计算出 A2了。
A2 = 0.5 * acceleration * dt**2运动模型
这意味着我们的总位移 A1 + A2 可以用下式表示:
displacement = velocity * dt + 0.5 * acceleration * dt**2我们还知道,速度随着时间的推移而变化:
velocity = acceleration*dt这两个方程一起组成了恒定加速度的运动模型。